Shortcut to seniority
Home
Go to main page
Section level: Junior
A journey into the programming realm
Section level: Intermediate
The point of no return
Section level: Senior
Leaping into the unknown

Go to main page
A journey into the programming realm
The point of no return
Leaping into the unknown
Chapter warning
This chapter will contain some algorithms that are usually learned in school.
It is great if you're able to follow the problem and the solution, but if not, do not discourage yourself!
Algorithms are great for exposing you to different problem-solving techniques. However, you will not use them in your everyday programming, and if you actually do need one, you can always look them up on the internet.
Therefore, it's a good idea to read this chapter, but if you are stuck or simply get bored, feel free to go directly to Chapter 3 and come back later on.
Kruskall’s algorithm picks the smallest weight edge, that doesn’t cause any cycle with the MST that is built in the process.
Kruskal’s algorithm detects the MST through the following steps:
Let's assume we have some edges and weights associated with them.
First step is to sort based on the weight.
| Weight | Source | Destination |
|---|---|---|
| 1 | 7 | 6 |
| 2 | 8 | 2 |
| 2 | 6 | 5 |
| 4 | 0 | 1 |
| 4 | 2 | 5 |
| 6 | 8 | 6 |
| 7 | 2 | 3 |
| 7 | 7 | 8 |
| 8 | 0 | 7 |
| 8 | 1 | 2 |
| 9 | 3 | 4 |
| 10 | 5 | 4 |
| 11 | 1 | 7 |
| 14 | 3 | 5 |
Now that we have the weights sorted in increasing order, we take them one by one and look for cycles within the MST.
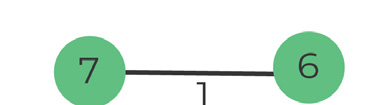
Pick edge 7-6, weight 1.
There is no cycle if we include it -> add to MST
Number of edges: 1
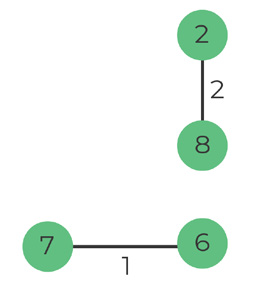
Pick edge 8-2, weight 2.
There is no cycle if we include it -> add to MST
Number of edges: 2
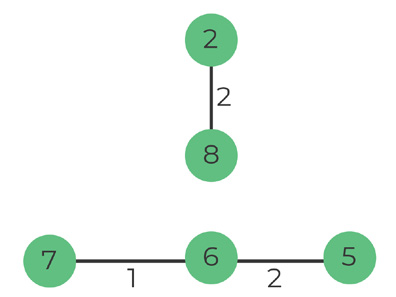
Pick edge 6-5, weight 2.
There is no cycle if we include it -> add to MST
Number of edges: 3
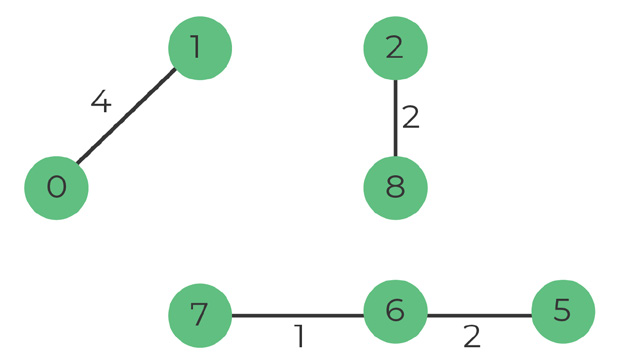
Pick edge 0-1, weight 4
There is no cycle if we include it -> add to MST
Number of edges: 4
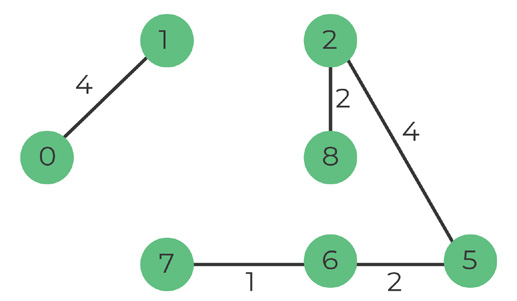
Pick edge 2-5, weight 4
There is no cycle if we include it -> add to MST
Number of edges: 5
Pick edge 8-6, weight 6
There is a cycle if we include it -> discard
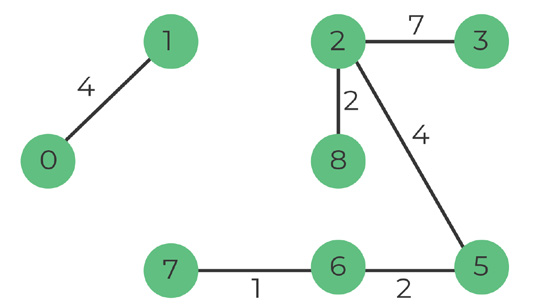
Pick edge 2-3, weight 7
There is no cycle if we include it -> add to MST
Number of edges: 6
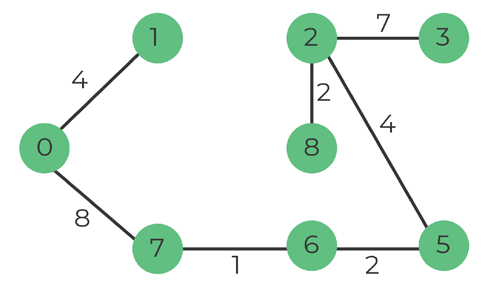
Pick edge 0-7, weight 8
There is no cycle if we include it -> add to MST
Number of edges: 7
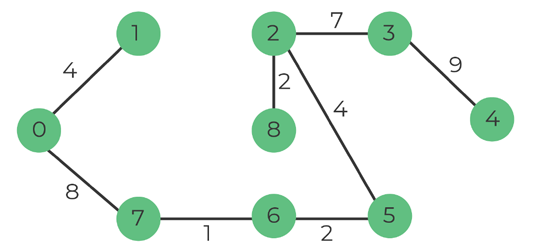
Pick edge 1-2
There is a cycle if we include it -> discard
Pick edge 3-4
There is no cycle if we include it -> add to MST
Number of edges: 8
After this last step, we have a MST with 8 edges, which is what we wanted, so the algorithm stops here.
struct Edge {
int from, to, cost;
};
class Graph {
public:
using GraphMap = vector<Edge>;
void addEdge(int from, int to, int cost) {
edges.push_back({ from, to, cost });
}
const GraphMap& getEdges() const { return edges; }
int kruskalMST();
private:
GraphMap edges;
};
bool sortingFunction(Edge& left, Edge&right) {
return left.cost < right.cost;
}
int Graph::kruskalMST() {
int result = 0;
sort(edges.begin(), edges.end(), sortingFunction);
UnionFindSets ufs(edges.size());
for (const Edge& edge : edges) {
int set_from = ufs.find(edge.from);
int set_to = ufs.find(edge.to);
// Check for cycle (exists in same set)
if (set_from != set_to) {
result += edge.cost;
ufs.merge(set_from, set_to);
}
}
return result;
}
int main() {
Graph graph;
graph.addEdge(0, 1, 4);
graph.addEdge(0, 7, 8);
graph.addEdge(1, 2, 8);
graph.addEdge(1, 7, 11);
graph.addEdge(2, 3, 7);
graph.addEdge(2, 8, 2);
graph.addEdge(2, 5, 4);
graph.addEdge(3, 4, 9);
graph.addEdge(3, 5, 14);
graph.addEdge(4, 5, 10);
graph.addEdge(5, 6, 2);
graph.addEdge(6, 7, 1);
graph.addEdge(6, 8, 6);
graph.addEdge(7, 8, 7);
std::cout << "Weight of MST is " << graph.kruskalMST();
return 0;
}
The algorithm starts at line 38, where the main() function is declared.
Further below, a graph is created and edges (connections from one vertex to another) are added in that graph.
In line 7 we create an alias so that a GraphMap refers to a vector of edges, so we will have information of the source and destination vertex, and the cost that it has.
Line 55 calls the Kruskall function, and we can find its implementation at line 20.
We initiate the result value with 0 (Line 21). That will be the cost of our MST.
Line 22 sorts the data based on a specific criteria (based on the cost). This means that, after the sort is finished, the vector will contain edges sorted by the cost to traverse that edge.
Line 24 introduces the UnionFindSets structure, and its implementation was explained before at the Cycle detection Chapter.
From there on, we iterate through all the edges one by one (Line 25), compare the sets of the source and destination for that given edge (Line 30), and if they are not part of the same set (in other words, if they don’t form a cycle) – we merge them together and add it to our final cost (Line 31-32).
Prim’s algorithm is a greedy algorithm that finds a minimum spanning tree within a graph (a subset of the graph that includes every vertex, in which the total weight of the edges is minimized).
This algorithm relies on keeping two sets of vertices, one being the vertices included in MST, while the other one keeping the remaining vertices.
At each step, the algorithm considers all the edges that connect two sets, picks the minimum weight edge, and adds the other endpoint of the edge to the first set (with the MST).
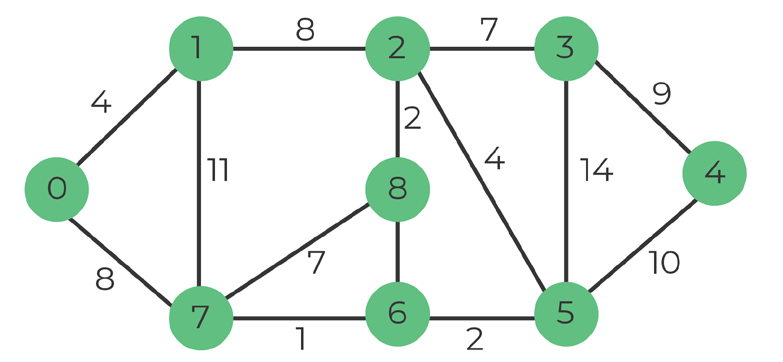
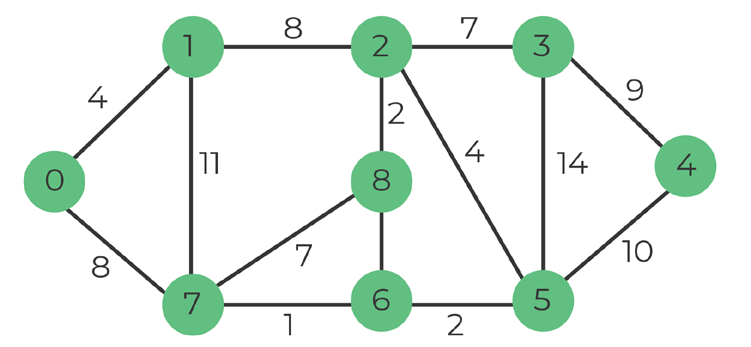
We have 9 vertices and 14 edges. The MST must have (9-1) = 8 edges
First step is to pick the vertex with the minimum key value, which is not included in MST. After the vertex is selected, we have to update the key values.
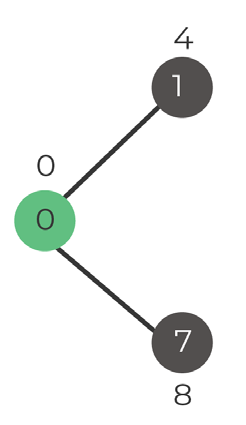
Step 1. Select vertex
Selected vertex 0
Set: 0
Step 2. Update key values
Vertex 1 = value 4
Vertex 7 = value 8
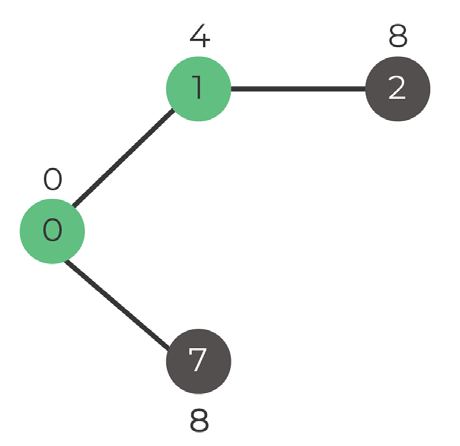
Step 1. Select vertex
Options:
Vertex 1 : value 4
Vertex 7 : value 8
Therefore, we pick vertex 1 and add it into the set
Set: 0, 1
Step 2. Update key values
Vertex 2 = value 8
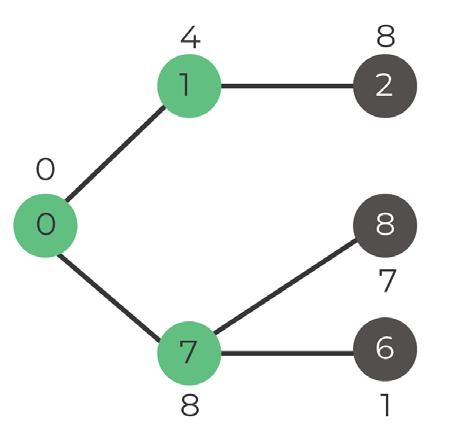
Step 1. Select vertex
Options:
Vertex 2: value 8
Vertex 7: value 8
We pick any of these two, let’s go with 7
Set: 0, 1, 7
Step 2. Update key values
Vertex 6 = value 1
Vertex 8 = value 7
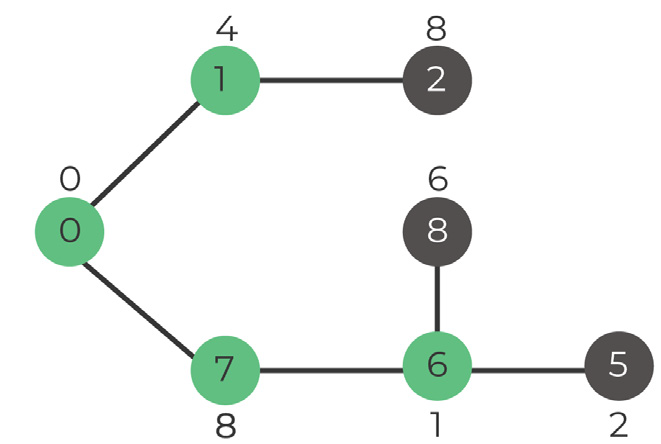
Step 1. Select vertex
Options:
Vertex 6: Value 1
Vertex 8: Value 7
We pick vertex 6 and add it into the set
Set: 0, 1, 7, 6
Step 2. Update key values
Vertex 5: value 2
Vertex 8: value 6
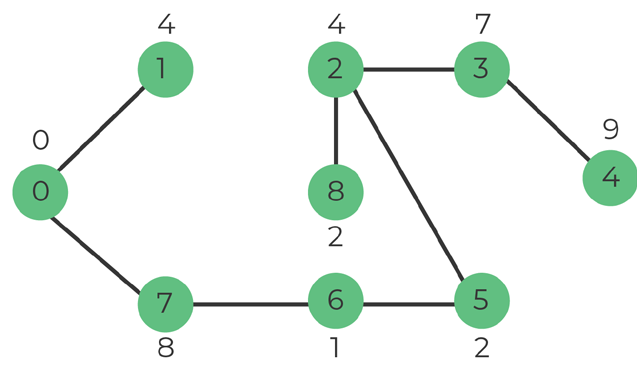
We repeat the steps until the set include all vertices of the graph
Assuming we have the following classes already defined:
struct Edge {
int to;
int cost;
bool operator >(const Edge& other) const {
return cost > other.cost || cost == other.cost && to > other.to; } };
class Graph {
public:
using GraphMap = map<int, vector<Edge>>;
void addEdge(int from, int to, int cost) {
vertices[from].push_back({ to, cost });
vertices[to].push_back({ from, cost });
}
const GraphMap& getVertices() const { return vertices; }
void primMST();
private:
GraphMap vertices;
};
int main() {
Graph graph;
graph.addEdge(0, 1, 4);
graph.addEdge(0, 7, 8);
graph.addEdge(1, 2, 8);
graph.addEdge(1, 7, 11);
graph.addEdge(2, 3, 7);
graph.addEdge(2, 8, 2);
graph.addEdge(2, 5, 4);
graph.addEdge(3, 4, 9);
graph.addEdge(3, 5, 14);
graph.addEdge(4, 5, 10);
graph.addEdge(5, 6, 2);
graph.addEdge(6, 7, 1);
graph.addEdge(6, 8, 6);
graph.addEdge(7, 8, 7);
graph.primMST();
return 0;
}
The classes from above will help us with the implementation, providing functionality for later usage.
void Graph::primMST() {
priority_queue<Edge, vector<Edge>, std::greater<Edge>> pq;
int src = 0;
int V_MAX = getVertices().size();
vector<int> key(V_MAX, numeric_limits<int>::max());
vector<int> parent(V_MAX, -1);
vector<bool> visited(V_MAX, false);
pq.push({ src, 0 });
key[src] = 0;
while (!pq.empty()) {
int node = pq.top().to;
pq.pop();
visited[node] = true;
for (auto& edge : getVertices().at(node)) {
int vertex = edge.to;
int weight = edge.cost;
if (visited[vertex] == false && key[vertex] > weight) {
pq.push({ vertex, weight });
parent[vertex] = node;
key[vertex] = weight;
}
}
}
cout << "From - To" << std::endl;
for (int i = 1; i < V_MAX; ++i)
cout << parent[i] << " - " << i;
}
Afterwards, we create a graph and add a few edges to it (Lines 23-37).
If we check the implementation of addEdge (Lines 10-13), we see that we fill the vertice nodes for both the source and the destination – therefore we are working with an undirected graph.
After the edges are added, we call the algorithm (Line 39).
The implementation of Prim’s algorithm starts at line 1.
In line 2 we see that we’ll be using a priority queue, which is nothing more than a binary heap. Based on the comparison function, we can make it either a min or a max heap.
Our priority queue uses a reverse comparison operator, so the edges will be sorted incrementally based on cost. (smallest cost will be on top of the queue).
Line 3 declares the source as 0, whereas line 4 is a constant which stores the number of vertices we have.
Afterwards, we create three vectors with the same size as our number of vertices:
Line 11 sets the key value for the source to 0 (no cost from this node to itself).
Until the priority queue is out of nodes (Line 13):
At the end of the algorithm:
That is because the entire loop is working with the vertex variable defined in line 20, which is the edge to the destination node.
Dijkstra’s Algorithm for calculating the shortest path is very similar to Prim’s algorithm.
Similar to Prim’s MST, we generate a shortest path tree (SPT) with given source as root, and we maintain two sets (one for vertices included in SPT, and another for the remaining vertices).
For each step of the algorithm, we find the vertex which is not included and has a minimum distance from the source.
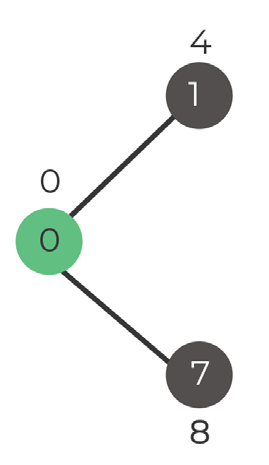
Step 1. Select vertex
Selected vertex 0
Set: 0
Step 2. Update distances
Vertex 1 = distance 4
Vertex 7 = distance 8
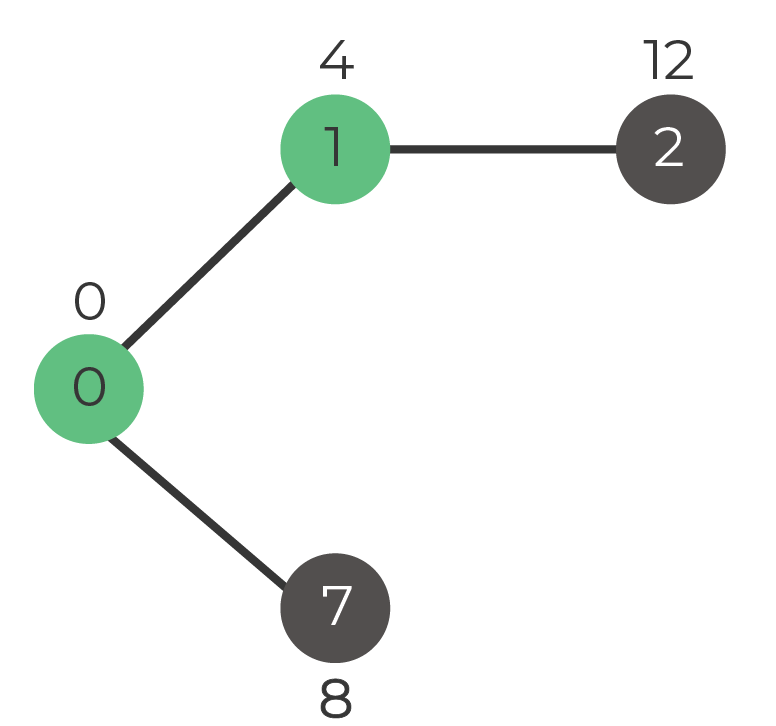
Step 1. Select vertex
Options:
Vertex 1: distance 4
Vertex 7: distance 8
We pick vertex 1
Set: 0, 1
Step 2. Update distances of adjacent vertices of 1
Vertex 2 = distance 12 (8+4)
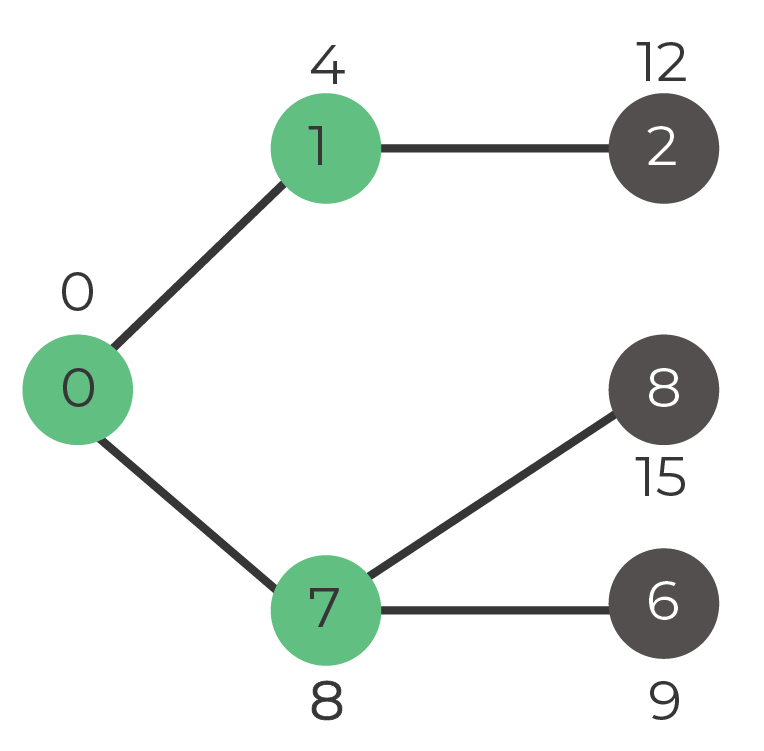
Step 1. Select vertex
Options:
Vertex 2: distance 12
Vertex 7: distance 8
We pick vertex 7
Set: 0, 1, 7
Step 2. Update distances of adjacent vertices of 7
Vertex 8 = distance 15 (8+7)
Vertex 6 = distance 9 (8+1)
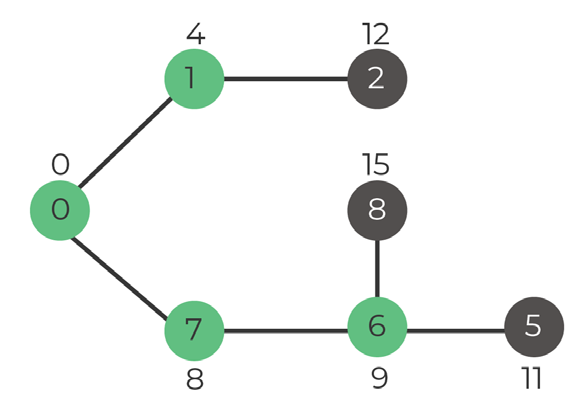
Step 1. Select vertex
Options:
Vertex 2: distance 12
Vertex 8: distance 15
Vertex 6: distance 9
We pick vertex 6
Set: 0, 1, 7, 6
Step 2. Update distances of adjacent vertices of 6
Vertex 8 = distance 15 (6+9)
Vertex 5 = distance 11 (2+9)
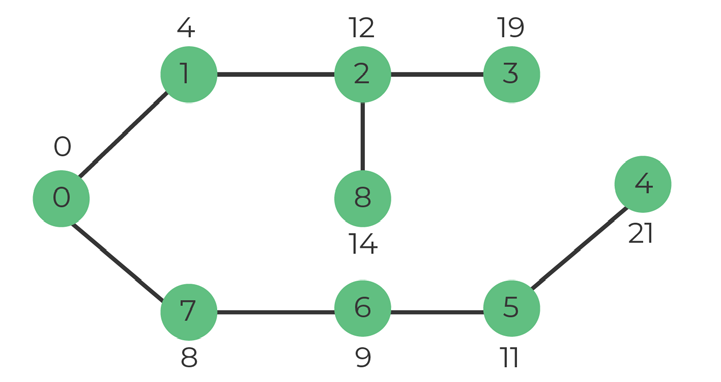
We repeat the steps until the set include all vertices of the graph.
This is how the distance from source will look like:
| Vertex | Distance from source |
|---|---|
| 0 | 0 |
| 1 | 4 |
| 2 | 12 |
| 3 | 19 |
| 4 | 21 |
| 5 | 11 |
| 6 | 9 |
| 7 | 8 |
| 8 | 14 |
If we are interested only in the shortest distance from the source to a specific target, we can stop the algorithm once we calculated the minimum distance for the target vertex.
void display(const map<int, int>& paths) {
for (const auto & path : paths)
cout << path.first << " - " << path.second << std::endl;
}
struct Edge {
int to;
int cost;
bool operator > (const Edge& other) const { return cost > other.cost; }
};
class Graph {
public:
using GraphMap = map<int, vector<Edge>>;
void addEdge(int from, int to, int cost) {
vertices[from].push_back({ to, cost });
vertices[to].push_back({ from, cost });
}
const GraphMap& getVertices() const { return vertices; }
private:
GraphMap vertices;
};
int main() {
Graph graph;
graph.addEdge(0, 1, 4);
graph.addEdge(0, 7, 8);
graph.addEdge(1, 2, 8);
graph.addEdge(1, 7, 11);
graph.addEdge(2, 3, 7);
graph.addEdge(2, 8, 2);
graph.addEdge(2, 5, 4);
graph.addEdge(3, 4, 9);
graph.addEdge(3, 5, 14);
graph.addEdge(4, 5, 10);
graph.addEdge(5, 6, 2);
graph.addEdge(6, 7, 1);
graph.addEdge(6, 8, 6);
graph.addEdge(7, 8, 7);
map<int, int> paths = shortestPath(graph.getVertices(), 0);
display(paths);
return 0;
}
The algorithm starts at line 26, where the main() function is declared.
Afterwards, we create a graph and add a few edges to it (Lines 27-41).
If we check the implementation of addEdge (Lines 15-18), we see that we fill the vertice nodes for the source and for the destination – therefore we are working with an undirected graph.After the edges are added, we call the algorithm (Line 43), and the implementation of it can be seen below.
map<int,int> shortestPath(const Graph::GraphMap& vertices, int src) {
priority_queue<Edge, vector<Edge>, std::greater<Edge>> pq;
map<int, int> dist;
pq.push({ 0, src });
dist[src] = 0;
while (!pq.empty()) {
int u = pq.top().to;
pq.pop();
for (const Edge &x : vertices.at(u)) {
const int dest = x.to;
const int cost = x.cost;
if (dist.find(dest) == dist.end() || dist.at(dest) > dist[u] + cost) {
dist[dest] = dist[u] + cost;
pq.push({ dest, dist[dest] });
}
}
}
return dist;
}
What we observe right from the start is the in and out of the function. We receive a map of vertices, and a starting point, and we return a map of integers (destination node, weight).
In line 2, we make use again of the priority_queue with the greater as comparison, so the edges will be sorted in increasing order based on the weight. In line 5-6 we add the source in the queue and we set the distance from source to itself as 0.
Until the queue is empty (Line 8):
The algorithm isn’t very hard, but we need to understand a few things:
In the end, the distance vector is what we actually return to the caller.
Knowing that the source node was 0, distance[0] will be 0, distance[1] will be the smallest cost to reach vertex 1 from vertex 0, etc.
A thief is robbing a house and can carry into his knapsack a maximal weight W.
There are N available items, each of them with their weight and profit of selecting that item. In fractional Knapsack, we can break the items to maximize the total value of knapsack. Which items should the thief take?
An efficient solution would be to use Greedy here. The basic idea is to calculate the value/weight ratio for each item, and sort them based on the highest ratio. Afterwards, we can use greedy and take the items with the highest ration.
Let’s assume the knapsack weight is 50.
Let’s define the following items (value / weight):
Let’s create the value/weight ratio.
Let’s sort based on ratio -> [Item1, Item2, Item3]
Let’s find out the maximum possible values:
We take item 1 (biggest ratio).
Total value = 60
Weight = 50-10 = 40
We take item 2
Total value = 60 + 100 = 160
Weight = 40-20 = 20
We don’t have enough weight left to fully take item 3, but we can take 2/3 of it
Total value = 160 + 2/3 * 120 = 160+80= 240
Weight = 20-2/3 * 30 = 20-20 = 0
Why 240 is the highet possible value?
We have only 3 items, of value 60, 100, and 120.
We cannot take all 3 of them, as that would result in a weight of 60, while the knapsack weight is 50.
Therefore, we can fill the knapsack by breaking the last item that would otherwise overflow the knapsack.
struct Item {
const double value, weight;
double ratio() const { return value / weight; }
bool operator <(const Item& other) const { return ratio() > other.ratio(); }
bool operator =(const Item& other) const { return weight == other.weight &&
value == other.value; }
};
double fractionalKnapsack(int maximumWeight, vector<Item>& items) {
sort(begin(items), end(items));
double currentWeight = 0;
double currentValue = 0.0;
for (const auto& item : items) {
// No overflow? Take as a whole
if (currentWeight + item.weight <= maximumWeight) {
currentWeight += item.weight;
currentValue += item.value;
}
else { // Overflow? Take only how much you can still fit in knapsack
double remainingWeight = maximumWeight - currentWeight;
currentValue += item.value * (remainingWeight / item.weight);
break;
}
}
return currentValue;
}
int main() {
int weight = 50;
vector<Item> items = { { 60, 10 }, { 100, 20 }, { 120, 30 } };
cout << fractionalKnapsack(weight, items);
return 0;
}
The code starts at line 31, in which the main() function is called.
We define a total weight our knapsack can have (Line 32) and a vector of items (Line 33). In line 1-7 we see that an item is defined as a pair of doubles (value and weight). The ratio is also important (Line 3), as we will use to assert how valuable an item is.
The algorithm starts in line 9, after being called from main().
The items are then sorted (Line 10), based on the comparison operator, or to be more specific, based on their ratio (Line 4). Because the comparison operator returns the bigger of two items, the vector will be sorted in decreasing order (the most valueable will be first).
We initiate two variables to keep track of the current weight and value we currently possess (Lines 12-13). Then, we iterate through the vector (Line 15), and we check whether we can steal the entire item (Line 17). If so, we add the weight to our weight counter, and its value to our value counter (Lines 18-19).
We repeat this for all the items in our knapsack.
At some point, the knapsack will be almost full, so we will no longer be able to add the entire item. (Line 21). Since the items are sorted by how valuable they are, it is clear that the current item we’re holding is more valuable then the remaining ones, so we verify the remaining weight that we have in the bag (Line 22), and steal only a part of that object. Therefore, the value counter will be increased with only a percentage of how much the item was valued, based on how much of it got stolen (if we stole half of an item of value 10, we increase our value with 5). This is done in line 23. Because we filled the knapsack with the remaining portion that can be filled, our knapsack is now full, so we can break out of the loop (Line 24).
Line 28 returns the value counter, which is the maximum value that we managed to steal with the current resources.
Vertex: Node containing data
Edge: The line that connects two vertices
Cycle: Cycles occur when nodes are connected in a way that they forms a closed structure.
Cycle: Cycles occur when nodes are connected in a way that they forms a closed structure.
Self loop: An edge that connects a vertex to itself (source = destination).
Divide et impera (Divide and conquer): Break the problem into sub-problems and solve them each recursively.
Negative weight edge refer to edges with a negative cost.