Shortcut to seniority

Section level: Senior

Leaping into the unknown

Chapter warning

This chapter will contain some algorithms that are usually learned in school.
It is great if you're able to follow the problem and the solution, but if not, do not discourage yourself!
Algorithms are great for exposing you to different problem-solving techniques. However, you will not use them in your everyday programming, and if you actually do need one, you can always look them up on the internet.
Therefore, it's a good idea to read this chapter, but if you are stuck or simply get bored, feel free to go directly to Chapter 3 and come back later on.

Tree traversal

Traversing a tree means that we visit every node in the tree. Every tree is a combination of a node carrying data, and two sub-trees.

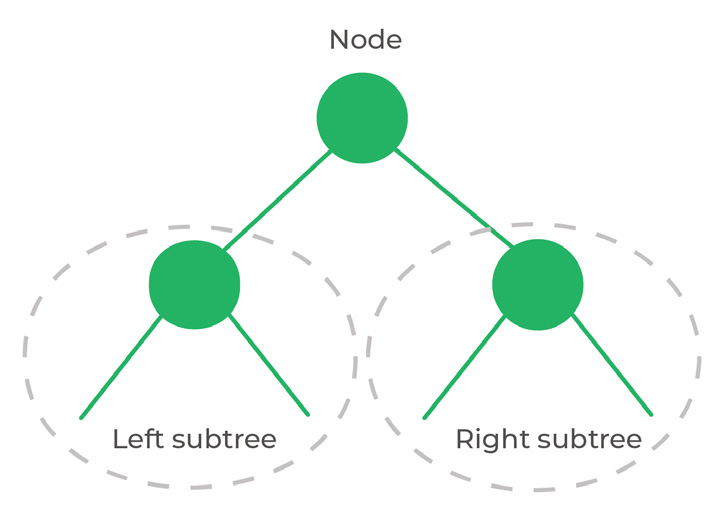
image with caption — Figure 26 Algorithms - Tree traversal

Depending on the order we visit all nodes, there are two big categories of traversals:

Depth first traversals, achieved through inorder, preorder, or postorder.
Breadth first traversals, achieved through level order.

Let’s assume that the definition of a node is as follows:


                                            struct Node {     
                                            Node(int data) : mData(data) {}     
                                                
                                            Node* left;    
                                            Node *right;   
                                            int mData;    
                                            };

We can see that the type is Node* - that is a pointer to an instance of type Node. In other words, we have reserved space for a pointer, so we can assign it afterwards to a memory address that stores a Node object.

Inorder

Inorder traversal is achieved by:

Visiting all the nodes in the left subtree
Visiting the root node
Visiting all the nodes in the right subtree


                                            void traversal_inorder(Node* node) {     
                                            if (node == nullptr)     
                                                return;     
                                                
                                            // go recursively on left side    
                                            traversal_inorder(node->left);     
                                                
                                            // consume the data for this node    
                                            cout << node->data << " ";     
                                                
                                            // go recursively on right side    
                                            traversal_inorder(node->right);     
                                            }

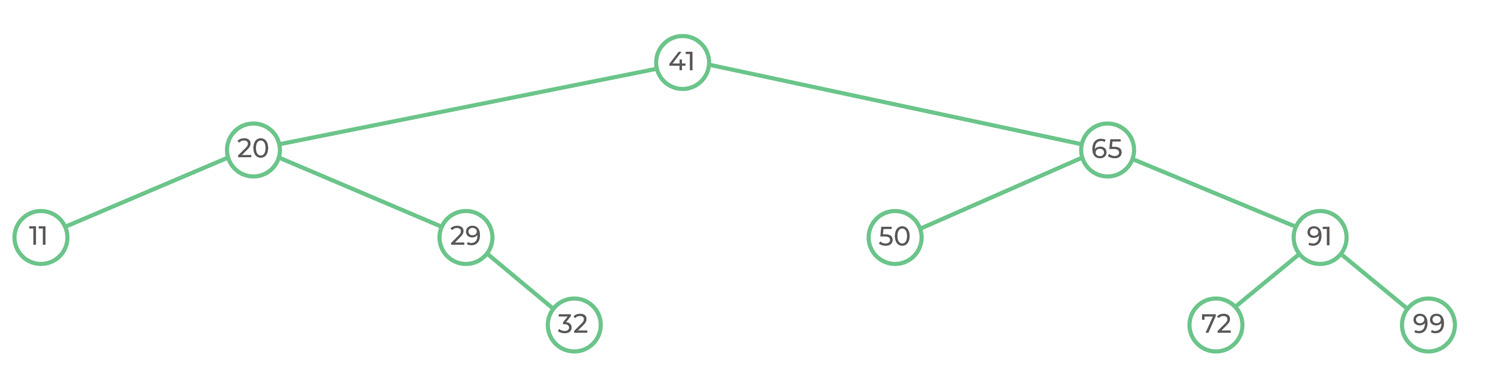
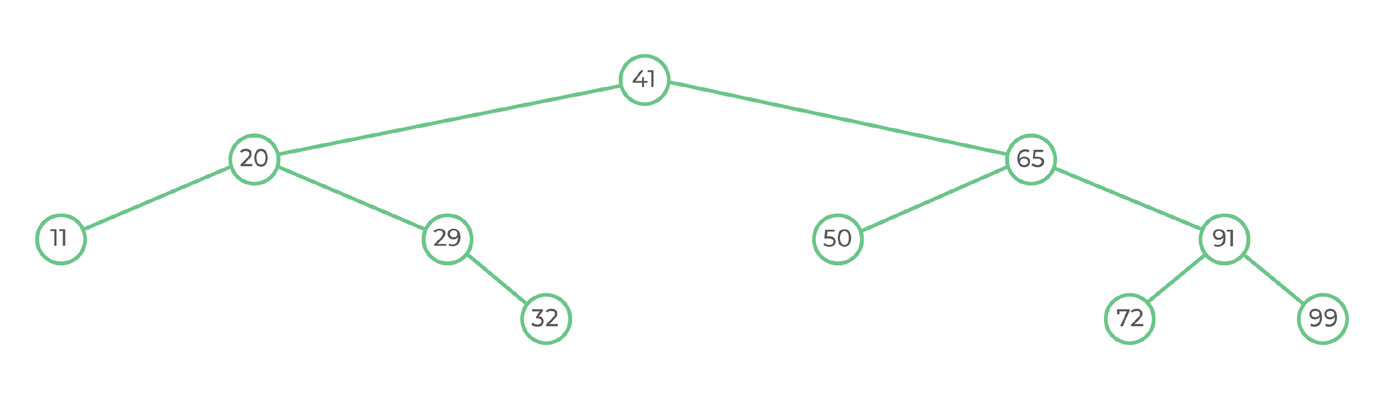
The function is called with the head node = 41.

According to the algorithm, we go to the left node until it is null, we print the data from that node and then we go right.

41 calls 20 which calls 11.
11 is done with the left side, so it displays itself {11} and goes to the right (null here, so it returns instead).
20 is done with the left side, so it displays itself {11, 20} and goes to the right (29).
29 is done with the left side, so it displays itself {11, 20,29} and goes to the right (32).
32 is done with the left side, so it displays itself {11, 20,29,32} and goes to the right (null here, so it returns instead).
41 is done with the left side, so it displays itself {11,20,29,32,41} and goes to the right (65) which calls 50.
50 is done with the left side, so it displays itself {11, 20,29,32,41, 50} and goes to the right (null here, so it returns instead).
65 is done with the left side, so it displays itself {11, 20,29,32,41, 50,65} and goes to the right (91) which calls 72.
72 is done with the left side, so it displays itself {11, 20,29,32,41, 50,65,72} and goes to the right (null here, so it returns instead).
91 is done with the left side, so it displays itself {11, 20,29,32,41, 50,65, 72, 91} and goes to the right (99).
99 is done with the left side, so it displays itself {11, 20,29,32,41, 50,65, 72, 91, 99} and goes to the right (null here, so it returns instead).

The stack unrolls until the last function is removed from the stack.
In-order traversal displays the following data: 11, 20, 29, 32, 41, 50, 65, 72, 91, 99.

Preorder

Preorder traversal is achieved by:

Visiting the root node
Visiting all the nodes in the left subtree
Visiting all the nodes in the right subtree


                                            void traversal_preorder(Node* node) {     
                                            if (node == nullptr)     
                                                return;     
                                                
                                            // consume the data for this node    
                                            cout << node->data << " ";     
                                                    
                                            // go recursively on left side    
                                            traversal_preorder(node->left);     
                                                
                                            // go recursively on right side    
                                            traversal_preorder(node->right);     
                                            }

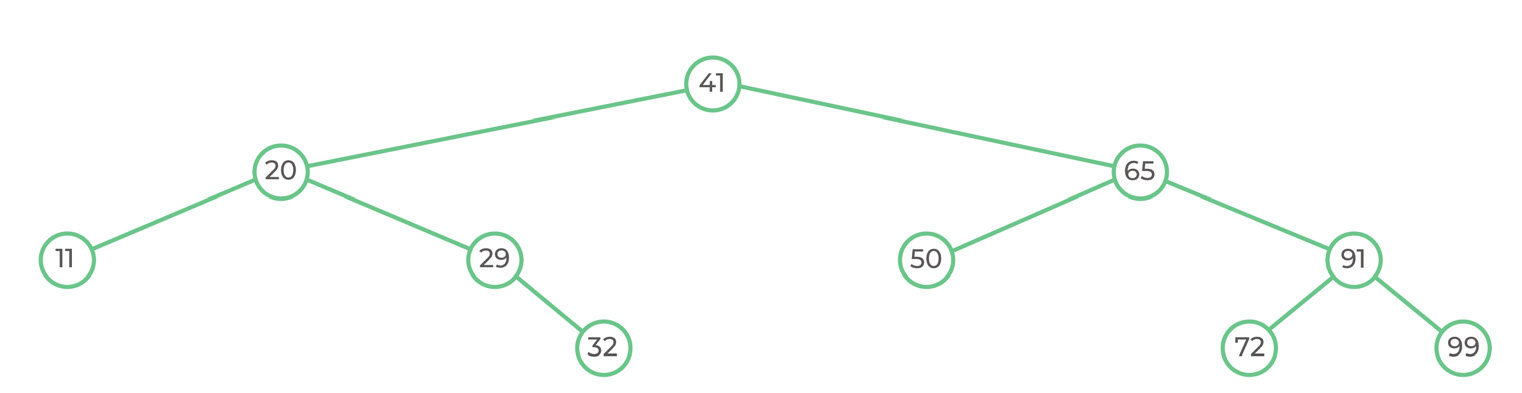
The function is called with the head node = 41.

According to the algorithm, we print the data and then go left side recursively, and then go right side recursively.

41 displays itself {41} and goes left side (20).
20 displays itself {41, 20} and calls left side (11).
11 displays itself {41, 20, 11} and has no items to the left nor right, so it goes back to the caller (20) which goes right side now (29).
29 displays itself {41, 20, 11, 29} and goes left side (nothing there) so it goes right side (32).
32 displays itself {41, 20, 11, 29, 32} and have nothing left nor right, so it goes back to the caller (29) -> back to the caller (20) -> back to the caller (41).
Now that 41 is done with the left side, it goes to the right (65).
65 displays itself {41, 20, 11, 29, 32, 65} and goes left (50).
50 displays itself {41, 20, 11, 29, 32, 65, 50} and have nothing to the left nor right, so it goes back to the caller (65) which goes right side now (91).
91 displays itself {41, 20, 11, 29, 32, 65, 50, 91} and goes left (72).
72 displays itself {41, 20, 11, 29, 32, 65, 50, 91, 72} and have nothing to the left nor right, so it goes back to the caller (91), which goes right side now (99).
99 displays itself {41,20,11,29,32, 65,50,91,72,99} and have nothing left nor right, so it goes back to the caller (91) -> back to the caller (65) -> back to the caller (41) -> pop out of the stack.

Pre-order traversal displays the following data: 41, 20, 11, 29, 32, 65, 50, 91, 72, 99.

Postorder

Postorder traversal is achieved by:

Visiting all the nodes in the left subtree
Visiting all the nodes in the right subtree
Visiting the root node


                                            void traversal_postorder(Node* node) {       
                                            if (node == nullptr)       
                                                return;       
                                                
                                            // go recursively on left side      
                                            traversal_postorder(node->left);       
                                                
                                            // go recursively on right side      
                                            traversal_postorder(node->right);       
                                                
                                            // consume the data for this node      
                                            cout << node->data << " ";       
                                            }

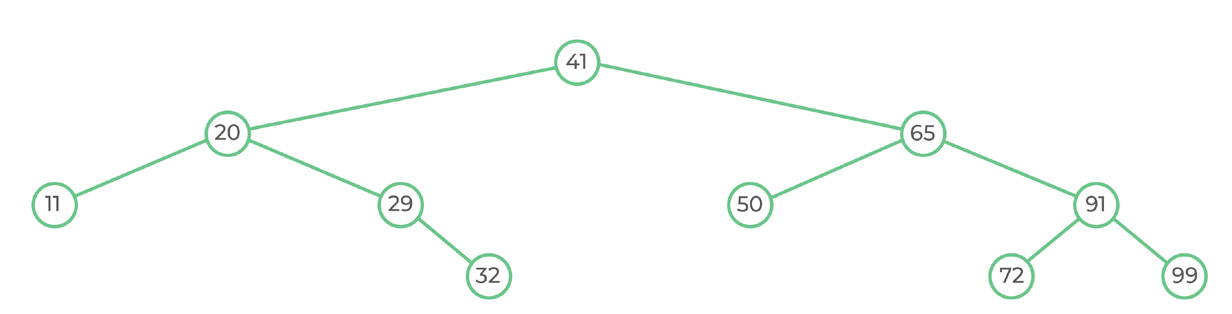
The function is called with the head node = 41.

According to the algorithm, we go left side recursively, then right side recursively, then we print the data.

41 goes left side (20).
20 goes left side (11).
11 have nothing on the left, nothing on the right, so it prints itself {11} and goes back to the caller (20).
20 goes right side (29).
29 have nothing on the left, so it goes on the right (32).
32 have nothing on the left, nothing on the right, so it prints itself {11, 32} and goes back to the caller (29).
29 displays itself {11, 32, 29} and goes back to the caller (20).
20 displays itself {11, 32, 29, 20} and goes back to the caller (41).
41 goes right side (65).
65 goes left side (50).
50 have nothing on the left or right, so it prints itself {11, 32, 29, 20, 50} and goes back to the caller (65).
65 goes right side (91).
91 goes left side (72).
72 have nothing on the left or right, so it prints itself {11, 32, 29, 20, 50, 72} and goes back to the caller (91).
91 goes right side (99).
99 have nothing on the left or right, so it prints itself {11, 32, 29, 20, 50, 72, 99} and goes back to the caller (91).
91 displays itself {11, 32, 29, 20, 50, 72, 99, 91} and goes back to the caller (65).
65 displays itself {11, 32, 29, 20, 50, 72, 99, 91, 65} and goes back to the caller (41).
41 displays itself {11, 32, 29, 20, 50, 72, 99, 91, 65, 41} and pops out of the stack.

Post-order traversal displayed the following data: 11, 32, 29, 20, 50, 72, 99, 91, 65, 41.

Level order

Level order traversal is achieved by visiting all nodes at a particular level, before visiting the nodes at a deeper level. In order to implement such traversal, we will need to use a queue. As we visit a node, we can add all the children in the queue, to visit them later as well. As long as the queue is not empty, we can take out a node from the front of the queue, visit it, and then enqueue its children.


                                            void traversal_levelorder(Node* root) {    
                                            if (root == nullptr) 
                                                return;  

                                            queue<Node*> traversal_queue;    
                                            traversal_queue.push(root);    
                                                
                                            while (!traversal_queue.empty()) {    
                                                Node* front = traversal_queue.front();    
                                                
                                                // use the current node    
                                                cout << front->data << " ";    
                                                
                                                // add the children of this node in the queue    
                                                traversal_queue.push(front->left);    
                                                traversal_queue.push(front->right);    
                                                
                                                // dispose the object    
                                                traversal_queue.pop();    
                                            }    
                                            }

We first create a queue that will store the nodes that we still have to visit, and then we add there the root node (41). The queue is not empty, so we pop the item from the queue, and add its children instead. Therefore, after the first run, we will have the first level traversed (the root node), and we have its left and right children in the queue {20, 65}.

For the 2^nd iteration, we pop the first item in the queue, which is 20. Now, the queue contains only the value 65. By adding the left and right children (next depth) to the queue, the queue will be {65, 11, 29}.

We can see that we cannot visit the next level until all the items from level 2 are visited yet. Level-order traversal displays the following data: 41, 20, 65, 11, 29, 50, 91, 52, 72, 99.

Shortcut to seniority

Badea Robert